Power Observation on Grids
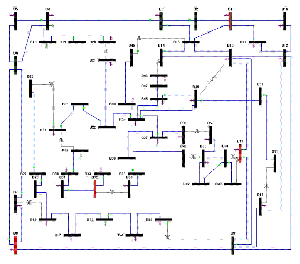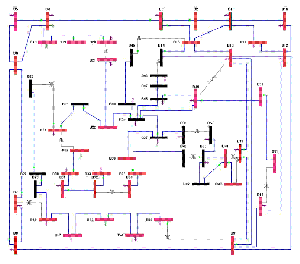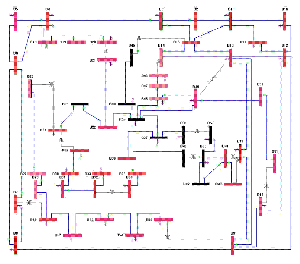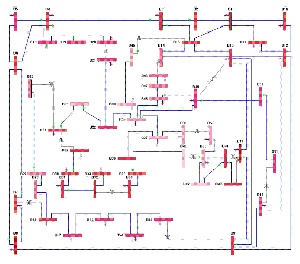When the global energy crisis and related issues become critically important, more researchers focus on the energy management problems and especially, Smart Grid is one of the most popular research topics. In order to solve the technical challenges of communications between power plants and stations, power companies have to observe the real-time state of a power grid and continually monitor the whole electricity system. The PMU (phasor measurement unit) was invented and such devices can measure the electrical waves on a power grid and determine the health of the utility system. We consider the power observation problem of optimally placing PMU devices on wide-area power grids according to different objectives, while maintaining the ability to observe electricity systems. (more details)
Capacitated Facility Location
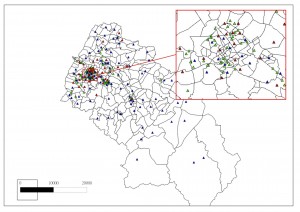With the rapid growth of international logistics market, one of the most important research issues is designing a large-scale distribution network. The question of large-scale distribution network design is also becoming central to globalization supply chain management. In general, the location and network design problems have become more important and have been studied extensively during the last decade. In order to deal with different real-world applications in which the constraints and requirements appear in different scenarios, these problems can be formulated in various ways. We study capacitated facility location in large-scale networks and its application to distribution network design. In a distribution network, each distribution center or client has associated with a demand, and each plant or facility has a capacity that specifies the maximum service the plant can provide to its distribution centers. (more details)
Three-dimensional Bin Packing
The bin packing problem is one of the classic NP-hard combinatorial optimization problems. Given a set of n items with positive sizes, the objective is to find a packing in bins of equal capacity to minimize the number of bins required. The problem finds obvious practical usage in many industrial applications, such as the container loading problem and the cutting stock problem. There are also many variations of the bin packing problem, such as the strip packing, square packing and rectangular box packing problems. We consider the three-dimensional orthogonal bin packing problem and present new lower bounds for the problem from a combinatorial point of view. In particular, we demonstrate that the bounds theoretically dominate all previous results from the literature. The comparison is also done concerning asymptotic worst-case performance ratios. The new lower bounds can be more efficiently computed in polynomial time. In addition, we study the non-oriented model, which allows items to be rotated. (more details)