When the global energy crisis and related issues become critically important, more researchers focus on the energy management problems and especially, Smart Grid is one of the most popular research topics. A smart grid is a representation form of an electricity network including a variety of digital technologies: for example, communications between power plants, transmission, distribution, and consumption, integration with different and intermittent renewable energy (like: wind power, solar power, hydropower, and so on) to maintain its stability, the reduction of electricity outage in power grids, and so on. In order to solve all of the above technical challenges, power companies have to observe the real-time state of a power grid and continually monitor the whole electricity system. The PMU (phasor measurement unit) was invented and such devices can measure the electrical waves on a power grid and determine the health of the utility system. Moreover, if we integrate GPS (global position system) into PMUs, then the PMUs can synchronously measure all the states and manage the power quality of the utility system.
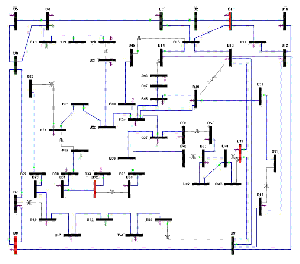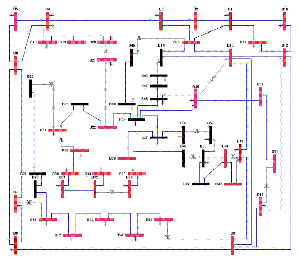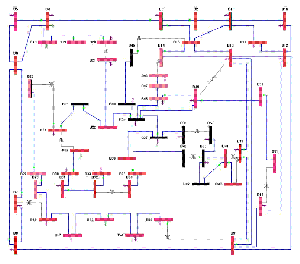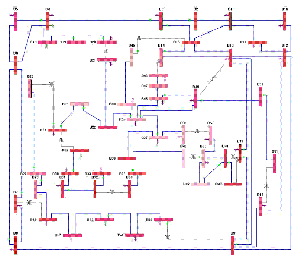
From an algorithmic perspective, we transform the practical power observation problem to a graph-theoretic combinatorial optimization problem (that is, the power domination problem) of optimally placing PMU devices in large-scale networks according to different objectives, while maintaining the ability to observe electricity systems. We focus on provably good approximation algorithms using analytical techniques and on empirical solutions, if appropriate, based on experimental study. Since power domination has been proved that its approximation threshold is quite large, we study efficient polynomial algorithms for network/graphs with special properties. We have shown that the power domination problem for split graphs (a subclass of chordal graphs) is NP-hard [6]. Linear time algorithms have also been presented for solving the power domination problem for both interval graphs and circular-arc problem, provided that the endpoints of the corresponding interval model or circular-arc model have been given sorted [5, 6].
Because power domination can be considered as a dominating set with propagation, we investigate a generalization which limits the number of propagation iterations to a given positive integer, just like message passing protocols, i.e., propagation with a bounded time constraint [1]. Recently, we implement these algorithms to IEEE power test systems. The results demonstrate the superior performance of the proposed algorithm in regard to both computational time and solution quality [3].
In addition to theoretical approximation results, the interdisciplinary collaboration with experts in power engineering area and practical implementation of a PMU-based electricity system are well-expected.
1. Chung-Shou Liao. Power domination with bounded time constraints, Journal of Combinatorial Optimization, Vol. 31(2), (2016), pp. 725-742.
2. Xian-Chang Guo, Chung-Shou Liao, and Chia-Chi Chu. Optimal PMU Placements Under Propagation Depth Constraints by Mixed Integer Linear Programming, in Proc. the IEEE International Conference on Smart Grid Communications (SmartGridComm 2016), Sydney, Australia.
3. Chung-Shou Liao, Tsung-Jung Hsieh, Jian-Hong Liu, Xian-Chang Guo, and Chia-Chi Chu. Hybrid Search for the Optimal PMU Placement Problem on a Power Grid, European Journal of Operational Research, Vol. 243(3), (2015) pp. 985-994.
4. Xian-Chang Guo, Chung-Shou Liao, and Chia-Chi Chu. Distributed Algorithm for PMU Placement Under N-1 Line Outage Conditions, in Proc. the IEEE PES Asia-Pacific Power and Energy Engineering Conference (IEEE PES APPEEC 2015), Brisbane, Australia.
5. Chung-Shou Liao and D. T. Lee. Power domination in circular-arc graphs, Algorithmica, Vol. 65(2), (2013) pp.443-466.
6. Chung-Shou Liao and D. T. Lee, Power domination problem in graphs, in Proceedings of the 11th International Computing and Combinatorics Conference (COCOON’05) Kunming, China, LNCS 3595, pp. 818-828.